Точечные и интервальные оценки парных, частных и множественных коэффициентов корреляции, проверка их значимости

Парный коэффициент корреляции характеризует меру статистической зависимости между величинами.

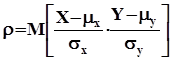- парный коэффициент корреляции,

Частный коэффициент корреляции характеризует линейную связь между двумя переменными случайными величинами независимо от влияния остальных случайных переменных.

Точечные оценки:

;;

;

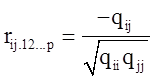
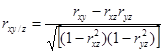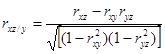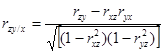интервальные оценки:

для парных коэффициентов используют статистику Фишера:

, надежность , доверительный интервал:

,

- находится по таблице Лапласа для

Множественный коэффициент корреляции характеризует меру связи между одной случайной величиной и остальными. Множественный коэффициент детерминации (квадрат коэф-та корр-ции) показывает долю дисперсии случайной величины х, обусловленную изменением остальных случайных величин.

Точечные оценки:

;;;;;;

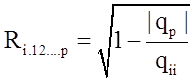
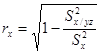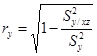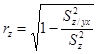проверка значимости:

,

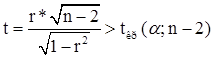для множественного R v=n-p.

проверка значимости множественного коэффициента детерминации (а также и множественного коэффициента корреляции) осуществляется с помощью F-распределения. Вычисляется:

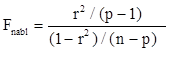
далее с заданным уровнем значимости α и числами степеней свободы ν1=p-1, и ν2=n-p находим Fтабл. Если Fnabl>Fтабл, то гипотеза H0:ρ2=0 отвергается с вероятностью ошибки α, то есть ρ2 значимо отличается от нуля.

Другие статьи

Технико-экономические показатели бумажной фабрики по производству писчей бумаги №1
бумага затрата прибыль рентабельность Бумажная промышленность - одна из крупнейших отраслей народного хозяйства. Продукция бумажной промышленности является материальной базой культурного развития страны и с каждым годом находит всё более широкое применение в ряде отраслей народного хозяйства. Бума ...