Интервальные оценки параметров генеральной совокупности

Дана выборка (x1, x2, …, xn) объема n из генеральной совокупности с генеральным средним a и генеральной дисперсией 2. Ищется интервал [Θ1, Θ2], в котором a может находиться с доверительной вероятностью γ.

Доверительный интервал для неизвестного математического ожидания a при известной дисперсии

Предполагая, что предварительно определена точечная оценка a - выборочное среднее , в качестве статистики для получения Θ1 = Θ1(x1, x2, …, xn) и Θ2=Θ2(x1, x2, …, xn) рассмотрим нормированное выборочное среднее , имеющее нормальное распределение ().

, где 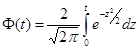- функция Лапласа.

Полагаем .

доверительный интервал:

.

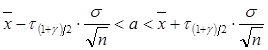Точность оценки: .

Доверительный интервал для неизвестного математического ожидания при неизвестной дисперсии

рассматривается нормированное выборочное среднее

,

где 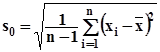- несмещенная оценка при неизвестном . Величина z имеет не зависящее от распределение Стьюдента с степенями свободы.

Доверительный интервал:

.

Точность оценки: .

Доверительный интервал для неизвестной дисперсии при известном математическом ожидании

В качестве статистики рассматривается величина

,

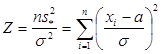где 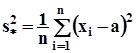- несмещенная оценка при известном . Функция имеет не зависящее от распределение с степенями свободы.

доверительный интервал:

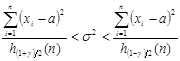
Доверительный интервал для неизвестной дисперсии при неизвестном математическом ожидании

.

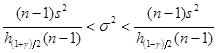
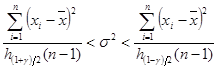Другие статьи

Финансово-хозяйственная деятельность ООО Торговая шинная компания
В современных условиях хозяйствования, где на первое место выходят такие понятия как эффективность, производительность, окупаемость, все больше внимания в работе предприятий уделяется увеличению эффективности ресурсов предприятия: трудовых и материальных, основных фондов и т.д. Руков ...