Множественные коэффициенты корреляции и детерминации, их свойства

Мерой тесноты линейной взаимосвязи между переменной и совокупностью остальных переменных служит множественный коэффициент корреляции (обобщение парного коэффициента корреляции ):

,

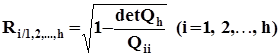где - определитель матрицы ;

- определитель матрицы, получающейся из матрицы удалением -ой строки и -го столбца.

В случае трехмерной корреляционной модели для переменных можно рассчитать три множественных коэффициента корреляции. В частности,

статистический вероятность дискретный экономический

.

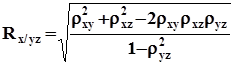Точечная оценка - выборочный множественный коэффициент корреляции:

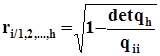
Выборочный множественный коэффициент детерминации.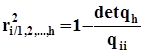 показывает долю дисперсии случайной величины , обусловленную изменением остальных переменных.

Свойства множественного коэффициента корреляции

.

Если , то связь между и остальными переменными является функциональной. В частном случае трехмерной корреляционной модели точки расположены в плоскости регрессии на .

Если , то случайная величина независима от других рассматриваемых переменных.

Множественный коэффициент корреляции не уменьшается при введении в модель дополнительных признаков и не увеличивается при исключении отдельных признаков из модели.

Для коэффициента детерминации функциональная связь возникает при значении равном 1, а отсутствие связи - 0. При значениях показателей тесноты связи меньше 0,7 величина коэффициента детерминации всегда будет ниже 50%. Это означает, что на долю вариации факторных признаков приходится меньшая часть по сравнению с остальными неучтенными в модели факторами, влияющими на изменение результативного показателя. Построенные при таких условиях регрессионные модели имеют низкое практическое значение.

Другие статьи

Характеристика предприятия ИП Кальчук Ю.А.
В соответствии с учебным планом я проходила производственную практику у ИП «Кальчук Ю.А» с30 апреля 2012 по 2 июня 2012 года. Я была принята для прохождения преддипломной практики на должность помощника юриста. В процессе прохождения практики я ознакомилась: с уставом пред ...