Нормальный закон распределения случайной величины

Нормальное распределение (закон Гаусса)

Непрерывная случайная величина распределена по нормальному закону с параметрами и , если плотность вероятности данной величины имеет вид:

.

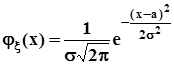Данное распределение вероятностей принято обозначать символом .

Нормальный закон распределения с параметрами , называется стандартным или нормированным (обозначается).

График плотности нормального распределения симметричен относительно вертикальной прямой, проходящей через точку оси абсцисс , и достигает в указанной точке максимума, равного ; имеет две точки перегиба .

Математическое ожидание случайной величины , подчиненной нормальному закону распределения, равно параметру , а её среднее квадратическое отклонение - параметру :

, .

Коэффициенты асимметрии и эксцесса случайной величины, подчиненной нормальному закону распределения, равны нулю.

Медиана и мода нормально распределенной случайной величины совпадают с её математическим ожиданием.

Интегральная функция распределения случайной величины , подчиненной нормальному закону распределения, связана с функцией Лапласа следующим соотношением:

.

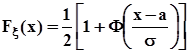«Правило трех сигм». X … (a-3σ, a+3σ).

Нормальное распределение является наиболее часто встречающимся в приложениях распределением. Причина такого широкого распространения этого закона заключается в том, что практически важные случайные величины слагаются из очень большого числа независимых случайных величин, каждая из которых лишь незначительно влияет на их сумму. Подобные суммы распределены почти по нормальному закону.

Другие статьи

Хозяйственная деятельность предприятий (организаций) в условиях рыночной экономики
Любое предприятие является связующим звеном, между возникающими потребностями людей и возможностями удовлетворения этих потребностей. Создаваясь, оно ставит перед собой задачу производство товаров, выполнение работ и услуг для потребления и имеет свой экономической целью создать более ...