Кластерная (сериальная) выборка

Сущность серийной выборки заключается в собственно-случайном или механическом отборе групп единиц (серий), внутри которых производится сплошное обследование. Единицей отбора служит группа или серия.

Средняя ошибка серийной выборки рассчитывается по ф-лам:

- повторный отбор , бесповторный отбор , где r - число отобранных серий, R - общее число серий.

Межгрупповая дисперсия при равновеликих группах вычисляется след образом:

,

где x(i) - средняя i - ой серии, x - общая средняя по всей выборочной совокупности.

Для определения необходимого объема выборки при заданной предельной ошибке используются след ф-лы:

повторный отбор , бесповторный отбор .

. Случайные величины. Закон распределение вероятностей дискретной случайной величины

Случайная величина - это измеримая функция, заданная на каком-либо вероятностном пространстве. Случайная величина - одно из основных понятий теории вероятностей.

Наряду со случайными событиями, как фактами в схеме испытаний, характеризующими её качественно, результаты опытов можно описать количественно. Это и ведёт к понятию случайной величины в теории вероятностей. Фактически, всегда результаты опытов со схемой можно представить количественно с помощью одной или нескольких числовых величин. Так, в конечных схемах описаний вместо самих элементарных исходов можно рассматривать их номиналы (идентификаторы). Например, при бросании монеты «решка» - это 0, а «орел» - это 1; при бросании игральной кости результаты - суть номера граней от 1 до 6 и т. п.

Переменная величина называется случайной, если в результате опыта она может принимать действительные значения с определёнными вероятностями.

Случайная величина Х называется дискретной, если существует такая неотрицательная функция

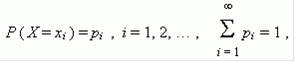
которая ставит в соответствие значению хi переменной Х вероятность рi, с которой она принимает это значение. Дискретные случайные величины X и Y называются независимыми, если события Х = хi и Y = yi при произвольных i и j являются независимыми.

Случайная величина Х называется непрерывной, если для любых a < b существует такая неотрицательная функция f ( x ), что

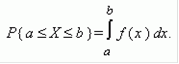
Закон распределения вероятностей дискретной случайной величины

Законом распределения случайной дискретной величины (X) называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины (x1,x2, .xn) и соответствующими им вероятностями (p1,p2, .,pn). При этом события (x1,x2, .xn) образуют полную группу (т.е. появление одного из них является достоверным событием), что означает

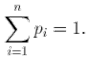(1)

Про случайную величину X в таком случае говорят, что она подчинена данному закону распределения.

Если множество возможных значений Х бесконечно (счетно), то ряд сходится и его сумма равна единице.

Простейшей формой задания этого закона является таблица, в которой перечислены возможные значения случайной величины и соответствующие им вероятности:

Другие статьи

Финансово-хозяйственная деятельность ОАО НК Роснефть-Дагнефть
Современный период характеризуется процессом утраты большинством промышленных предприятий части собственных оборотных средств и, как следствие, непрекращающимся платежным кризисом. Высокий уровень инфляции, обесценивающей будущие доходы, и отсутствие механизма пополнения оборотных ср ...